【翻译】 深入理解以太坊虚拟机 - 如何表示动态数据类型
原文:https://medium.com/@hayeah/diving-into-the-ethereum-vm-the-hidden-costs-of-arrays-28e119f04a9b
译者:中山大学数学学院(珠海)林学渊
大二时给量子做的翻译,转载注明出处,谢谢
如何表示动态数据类型
数组的隐性成本
Solidity 提供了我们熟悉的数据结构。除了简单的如数字和结构体,也有其他数据类型,它们能随着数据的添加而动态变化。3个主要的动态类型是:
- 映射:
mapping(bytes32 => uint256),mapping(address => string),等等。 - 数组:
[]uint256,[]byte,等等。 - 字节数组:只有两种,字符串和字节。
在本系列第二篇文章中,我们已经看到固定长度的简单类型在存储中是如何表示的。
- 基础类型:
uint256,byte,等等。 - 定长数组:
[10]uint8,[32]byte,bytes32。 - 结构体:用以上两种类型组装而成。
固定长度的存储变量在存储中一个接一个存储,尽可能轻量地打包成32字节的块。
如果对这个不熟,我建议看: Diving Into The Ethereum VM Part II — Storage Cost
在这篇文章中,我们深入理解 Solidity 是如何支持更多复杂的数据结构的。 Solidity 中的数组和映射可能看起来很熟悉,但它们的实现方式使它们具有本质的不同。
我们从映射开始,这是三者中最简单的一种。 事实证明,数组和字节数组只是有更多的功能的映射。
映射
在 uint256 => uint256 映射中存储一个值:1
2
3
4
5
6
7pragma solidity ^0.4.11;
contract C {
mapping(uint256 => uint256) items;
function C() {
items[0xC0FEFE] = 0x42;
}
}
编译:1
solc --bin --asm --optimize c-mapping.sol
汇编代码:1
2
3
4
5
6
7
8
9
10
11
12
13tag_2:
// 什么也没干. 可以优化.
0xc0fefe
0x0
swap1
dup2
mstore
0x20
mstore
// 存储 0x42 到地址 0x798...187c
0x42
0x79826054ee948a209ff4a6c9064d7398508d2c1909a392f899d301c6d232187c
sstore
我们可以将 EVM 存储视为键值对数据库,每个键限制为 32 个字节。不是直接使用键 0xC0FEFE ,而是将键散列为 0x798...187c,并将值 0x42 存储在那里。使用的哈希函数是 keccak256(SHA256)。
在这个例子里,我们没有看到 keccak256 指令,因为优化器已经预先计算结果并将其内联到字节码里了。可以从这些没用的 mstore 指令中看到这种计算的痕迹。
计算地址
让我们用一些 Python 代码来将 0xC0FEFE 散列为 0x798...187c。如果你想跟着做,你需要 Python 3.6,或者安装 pysha3 来获得 keccak_256 哈希函数。
定义两个辅助函数:
1 | import binascii |
把一个数转化为 32 字节的数组:1
2
3
4>> bytes32(1)
b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01'
>> bytes32(0xC0FEFE)
b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xc0\xfe\xfe'
用 + 运算把两个字节数组接在一起:1
2>> bytes32(1) + bytes32(2)
b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x02'
计算字节数组的 keccak256 哈希1
2>> keccak256(bytes(1))
'bc36789e7a1e281436464229828f817d6612f7b477d66591ff96a9e064bcc98a'
现在我们可以计算 0x798...187c了。
存储变量 items 的位置是 0x0(因为它是第一个存储变量)。要获取地址,将键 0xc0fefe 与 items 的位置接在一起:1
2
3
>>> keccak256(bytes32(0xC0FEFE) + bytes32(0))
'79826054ee948a209ff4a6c9064d7398508d2c1909a392f899d301c6d232187c'
计算一个键的存储地址的公式为:1
keccak256(bytes32(key) + bytes32(position))
2 个映射
让我们用公式来计算值会存储到哪个位置!假设我们有2个映射:
1 | pragma solidity ^0.4.11; |
itemsA 的位置为 0, 键为 0xAAAA:1
2
3 key = 0xAAAA, position = 0
>> keccak256(bytes32(0xAAAA) + bytes32(0))
'839613f731613c3a2f728362760f939c8004b5d9066154aab51d6dadf74733f3'
itemsB 的位置为 1, 键为 0xBBBB:1
2
3 key = 0xBBBB, position = 1
>> keccak256(bytes32(0xBBBB) + bytes32(1))
'34cb23340a4263c995af18b23d9f53b67ff379ccaa3a91b75007b010c489d395'
我们用编译器证明我们的计算:1
solc --bin --asm --optimize c-mapping-2.sol
汇编代码:1
2
3
4
5
6
7
8tag_2:
// ... 忽略内存优化,可以优化掉
0xaaaa
0x839613f731613c3a2f728362760f939c8004b5d9066154aab51d6dadf74733f3
sstore
0xbbbb
0x34cb23340a4263c995af18b23d9f53b67ff379ccaa3a91b75007b010c489d395
sstore
和我们想的一样。
汇编里的 KECCAK256
编译器能预先计算一个键的地址,因为涉及的键是常量。如果键是一个变量,那么散列需要用汇编代码完成。现在我们要禁用这个优化,以便看到哈希如何在汇编中完成。
事实证明,通过引入一个额外变量 i 可以简化优化器:
1 | pragma solidity ^0.4.11; |
变量位置还是 0x0, 所以我们认为地址和前面一样。
编译,但这次没有哈希预计算:1
$ solc --bin --asm --optimize c-mapping--no-constant-folding.sol
汇编代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45tag_2:
// `i` 入栈
sload(0x1)
[]
// 存储键 `0xC0FEFE` 到内存 0x0, 准备哈希.
0x0
[]
swap1
[]
dup2
[]
mstore
[]
memory: {
0x00 => 0xC0FEFE
}
// 保持位置 `0x0` 到内存 0x20 (32), 准备哈希.
0x20 // 32
[]
dup2
[]
swap1
[]
mstore
[]
memory: {
0x00 => 0xC0FEFE
0x20 => 0x0
}
// 从第 0 个字节开始,依次哈希内存中接下来的 0x40 (64) 字节
0x40 // 64
[]
swap1
[]
keccak256
[]
// 保存 0x42 到计算地址
0x42
[]
swap1
[]
sstore
store: {
0x798...187c => 0x42
}
mstore 指令在内存中写入 32 个字节。 内存要便宜得多,只需要 3 gas 来读写。汇编代码前半部分通过将键和位置加载到相邻的内存块中来“连接”键和位置:1
2 0 31 32 63
[ key (32 bytes) ][ position (32 bytes) ]
然后,keccak256 指令散列该内存区域中的数据。成本取决于有多少数据被散列:
- 30 付给每个SHA3操作。
- 6 付给每个32字节的字。
对于 uint256 键,gas 成本是 42(30 + 6 * 2)。
映射大数值
每个存储单元只能存储 32 个字节。如果试图存储更大的结构会发生什么?
1 | pragma solidity ^0.4.11; |
编译,你可以看到 3 个 sstore 指令:1
2
3
4
5
6
7
8
9
10
11tag_2:
// ...忽略未优化代码
0x1a
0xada5013122d395ba3c54772283fb069b10426056ef8ca54750cb9bb552a59e7d
sstore
0x1b
0xada5013122d395ba3c54772283fb069b10426056ef8ca54750cb9bb552a59e7e
sstore
0x1c
0xada5013122d395ba3c54772283fb069b10426056ef8ca54750cb9bb552a59e7f
sstore
注意,除了最后一位数字,计算出的地址都是相同的。Tuple 结构的字段一个接一个地排列(.7d,.7e,.7f)。
映射不打包
由于映射的设计方式,即使只存储 1 个字节,每一项的最小存储量也是 32 个字节:
1 | pragma solidity ^0.4.11; |
如果值大于 32 字节,则以 32 字节为单位支付存储费用。
动态数组是 Mappings++
(译者注:C和C++的梗)
在经典程序语言中,数组只是一个在内存中连续排列数据项的列表。假设你有一个含 100 个 uint8 元素的数组,那么它将占用 100 个字节的内存。在此方案中,将整个阵列批量加载到 CPU 缓存中并循环遍历项目很便宜。
对于大多数语言而言,数组比映射便宜。不过,对于 Solidity 而言,数组是一种更昂贵的映射。数组的数据项按顺序放置在存储中,如:1
2
3
40x290d...e563
0x290d...e564
0x290d...e565
0x290d...e566
但记住,每次对这些存储单元的访问实际上都是数据库中的键值查找。访问数组元素与访问映射元素没有区别。
考虑类型 [] uint256,它与映射(uint256 => uint256)基本相同,并增加了使其“类似数组”的功能:
length表示有多少数据项。- 绑定检查。读取或写入超出长度的索引时会引发错误。
- 比映射更复杂的存储打包行为。
- 数组缩小时自动释放未使用的存储单元。
- 对
bytes和string进行特殊优化,使短数组(小于31字节)的存储效率更高。
简单数组
我们来看看存储三个数据项的数组:1
2
3
4
5
6
7
8
9
10// c-darray.sol
pragma solidity ^0.4.11;
contract C {
uint256[] chunks;
function C() {
chunks.push(0xAA);
chunks.push(0xBB);
chunks.push(0xCC);
}
}
数组访问的汇编代码太复杂,无法跟踪。我们用 Remix 调试器来运行合约:
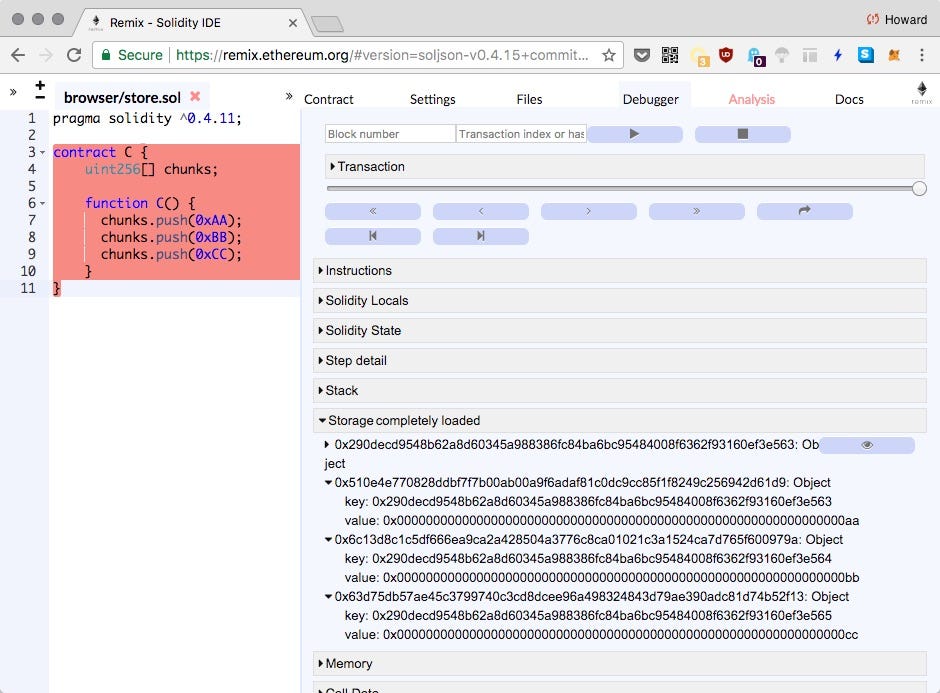
可以看到使用了 4 个存储单元:1
2
3
4
5
6
7
8key: 0x0000000000000000000000000000000000000000000000000000000000000000
value: 0x0000000000000000000000000000000000000000000000000000000000000003
key: 0x290decd9548b62a8d60345a988386fc84ba6bc95484008f6362f93160ef3e563
value: 0x00000000000000000000000000000000000000000000000000000000000000aa
key: 0x290decd9548b62a8d60345a988386fc84ba6bc95484008f6362f93160ef3e564
value: 0x00000000000000000000000000000000000000000000000000000000000000bb
key: 0x290decd9548b62a8d60345a988386fc84ba6bc95484008f6362f93160ef3e565
value: 0x00000000000000000000000000000000000000000000000000000000000000cc
一个块的位置是 0x0,它用于存储数组的长度(0x3)。散列变量的位置以查找数组数据项的地址:1
2
3 position = 0
>> keccak256(bytes32(0))
'290decd9548b62a8d60345a988386fc84ba6bc95484008f6362f93160ef3e563'
数组中的每个数据项都从该地址(0x29..63,0x29..64,0x29..65)开始顺序布局。
动态数组打包
你怎么看这些所有重要的打包行为?基于映射的数组的一个优点是打包。 四个数据项的 uint128 [] 数组恰好填满两个存储单元(加 1 用于存储长度)。
考虑:1
2
3
4
5
6
7
8
9
10
11pragma solidity ^0.4.11;
contract C {
uint128[] s;
function C() {
s.length = 4;
s[0] = 0xAA;
s[1] = 0xBB;
s[2] = 0xCC;
s[3] = 0xDD;
}
}
在 Remix 上运行, 最终存储的状态是:1
2
3
4
5
6key: 0x0000000000000000000000000000000000000000000000000000000000000000
value: 0x0000000000000000000000000000000000000000000000000000000000000004
key: 0x290decd9548b62a8d60345a988386fc84ba6bc95484008f6362f93160ef3e563
value: 0x000000000000000000000000000000bb000000000000000000000000000000aa
key: 0x290decd9548b62a8d60345a988386fc84ba6bc95484008f6362f93160ef3e564
value: 0x000000000000000000000000000000dd000000000000000000000000000000cc
和我们想的一样,只用了 3 个存储单元。长度存储在 0x0 处,即存储变量的位置。四个数据项打包在两个独立的存储单元中。该数组的起始地址是变量位置的哈希值:
1 | position = 0 |
现在每增加两个数组元素,地址才会增加一次。看起来ok!
但汇编代码本身并没有得到很好的优化。由于只使用两个存储单元,因此我们希望优化器也只使用两个 sstore 进行分配。然而,在引入边界检查(以及其他)情况下,不可能优化 sstore 指令。
四个 sstore 指令用于分配:
1 | /* "c-bytes--sstore-optimize-fail.sol":105:116 s[0] = 0xAA */ |
字节数组 & 字符串
bytes 和 string 是分别针对字节和字符进行优化的特殊数组类型。如果数组的长度小于 31 个字节,则只用一个存储单元来存储整个数组。较长的字节数组与正常数组的表示方式大致相同。
我们来看一个实际使用的短字节数组:
1 | // c-bytes--long.sol |
由于数组只有 3 个字节(小于 31 个字节),因此它只占用一个存储单元。在 Remix 中运行,存储状态为:1
2key: 0x0000000000000000000000000000000000000000000000000000000000000000
value: 0xaabbcc0000000000000000000000000000000000000000000000000000000006
数据 0xaabbcc... 从左到右存储。后面的 0 是空数据。最后一个字节 0x06 是数组的编码长度。 公式为 encodedLength / 2 = length。这种情况下,实际长度是 6/2 = 3。
字符串的工作方式和这个完全相同。
长字节数组
如果数据量大于 31 字节,则字节数组就像 []byte。让我们看看长度为 128 字节的字节数组:1
2
3
4
5
6
7
8
9
10
11
12// c-bytes--long.sol
pragma solidity ^0.4.11;
contract C {
bytes s;
function C() {
s.length = 32 * 4;
s[31] = 0x1;
s[63] = 0x2;
s[95] = 0x3;
s[127] = 0x4;
}
}
在 Remix 运行,可以看到存储里使用了 4 个存储单元:1
2
3
4
5
6
7
8
9
100x0000...0000
0x0000...0101
0x290d...e563
0x0000...0001
0x290d...e564
0x0000...0002
0x290d...e565
0x0000...0003
0x290d...e566
0x0000...0004
存储单元 0x0 不再用于存储数据。整个存储单元现在存储编码后的数组长度。为了得到实际的长度,做 length =(encodedLength - 1)/ 2。在这种情况下,长度为 128 =(0x101 - 1)/ 2。实际字节存储在 0x290d...e563 中,以及按顺序排列的存储单元中。
字节数组的汇编代码非常大。除了正常的边界检查和调整数组大小的东西,它还要编码/解码长度,以及在长和短字节数组之间进行转换。
为什么要对长度进行编码?因为这种方式有一个简单的方法来检测一个字节数组是短还是长。注意,长数组的编码长度总是奇数,短数组的编码长度总是偶数。汇编只需要查看最后一位,看它是零(偶/短)还是非零(奇/长)。
小结
查看 Solidity 编译器的内部工作,我们发现熟悉的数据结构(如映射和数组)与传统的编程语言的完全不同。
回顾一下:
- 数组就像映射,效率不高。
- 比映射更复杂的汇编代码。
- 比较小类型(字节,uint8,字符串)映射更好的存储效率。
汇编代码没有很好地优化。即使打包过了,还是每个分配要一个 sstore 。
EVM 存储是一个键值对数据库,非常像 git。如果你改变了任何东西,那么根节点的校验和就会改变。如果两个根节点具有相同的校验和,则存储的数据相同。
要了解 Solidity 和 EVM 的独特之处,可以想象数组中的每个元素都是一个文件在 git 存储库中。当你改变一个数组元素的值时,你实际上正在创建一个 git commit。在遍历数组时,无法一次加载整个数组,您必须查看存储库并分别查找每个文件。
不仅如此,每个文件被限制为 32 个字节!因为我们需要将数据结构分割成32个字节的块,所以 Solidity 的编译器由于各种逻辑和优化技巧而复杂化,所有这些都是在汇编中完成的。
然而,32 字节的限制完全是任意的。备份键值存储可以使用键存储任意数量的字节。也许在将来我们可以添加一个新的 EVM 指令来存储任意字节和一个关键字。
目前,EVM 存储是一个预先假定为32字节数组的键值对数据库。
请参阅 ArrayUtils::resizeDynamicArray,了解编译器在调整数组大小时的作用。通常情况下,数据结构将作为标准库的一部分在语言中完成,但在 Solidity 中,它会被烧录入编译器。
如果你喜欢这篇文章,你应该在 Twitter @hayeah 上关注我。