网页排序算法(三)代数方法求PageRank
本文结合实例介绍如何用代数方法求PageRank。
博文《网页排序算法(一)PageRank》介绍了PageRank,计算PageRank可以用迭代的方法也可以用代数的方法,其背后的数学基本运算是一样的,即:
$$PR(pi)=\frac{1−d}{N}+d \sum{p_j\in B(p_i)} \frac{PR(p_j)}{L(p_j)}$$
下文结合图1介绍如何用代数方法求PageRank。
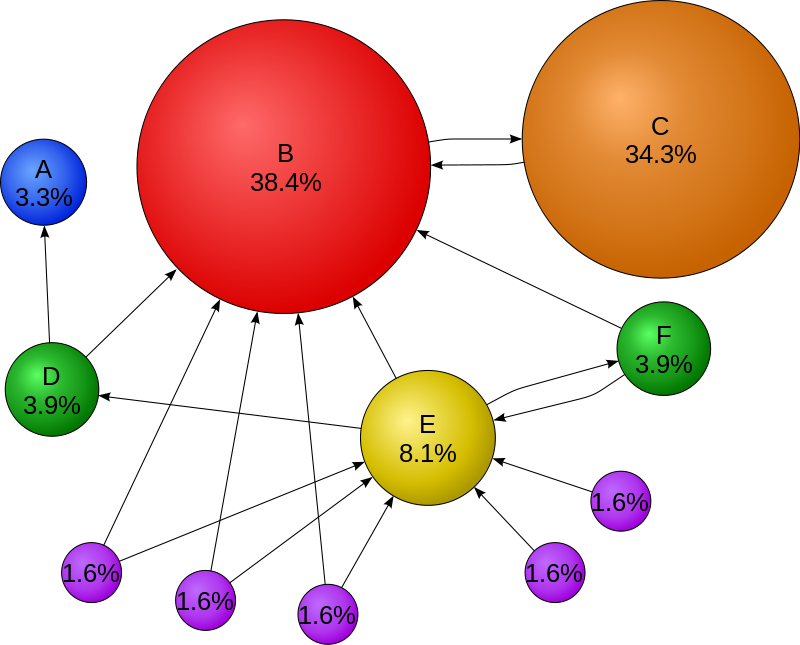
为了便于讨论,将图1下方的节点分别标上G, H, I, J, K,如下图所示:
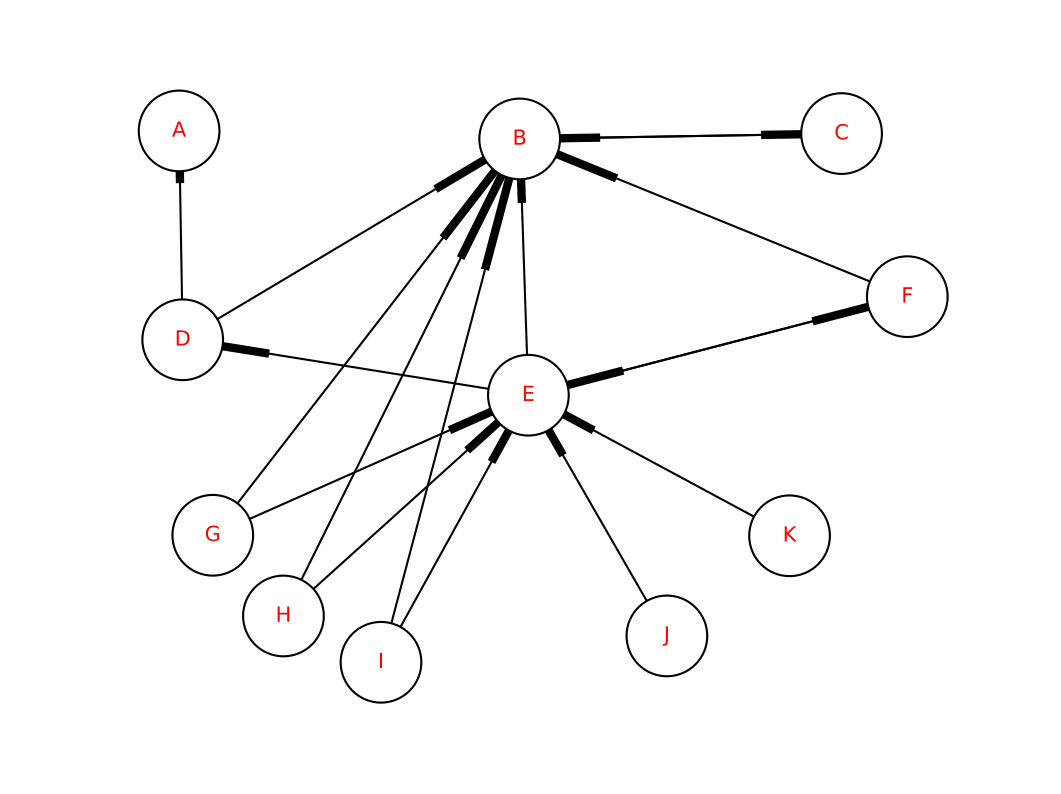
Fig. 2: Draw Fig. 1 in NetworkX.
代数方法
根据1中的等式,把所有节点都放在一块,可以得到:
$$\begin{bmatrix}
PR(p_1) \
PR(p_2) \
\vdots \
PR(p_3)
\end{bmatrix} =
\begin{bmatrix}
{(1-d)/ N} \
{(1-d) / N} \
\vdots \
{(1-d) / N}
\end{bmatrix}
- d
\begin{bmatrix}
\ell(p_1,p_1) & \ell(p_1,p_2) & \cdots & \ell(p_1,p_N) \
\ell(p_2,p_1) & \ddots & & \vdots \
\vdots & & \ell(p_i,p_j) & \
\ell(p_N,p_1) & \cdots & & \ell(p_N,p_N)
\end{bmatrix}
\begin{bmatrix}
PR(p_1) \
PR(p_2) \
\vdots \
PR(p_3)
\end{bmatrix}$$
上述等式可以缩写为:
$$\mathbf{R} = d \mathcal{M}\mathbf{R} + \frac{1-d}{N} \mathbf{1}. (**)$$
其中,1为N维的列向量,所有元素皆为1。以图1为例,该列向量为,1
2
3
4
5
6
7
8
9
10
11
12
13
14N = len(G.nodes()) # N = 11
column_vector = np.ones((N, 1), dtype=np.int)
[[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]
[1]]
Adjacency function
邻接函数(adjacency function)$$\ell(p_1,p_2)$$组成了矩阵M,
$$\mathcal{M}_{ij} =\ell(pi,pj) = \begin{cases} 1 /L(p_j) , & \mbox{if }j\mbox{ links to }i\ L(pj)是指从pj链出去的网页数目\ 0, & \mbox{otherwise} \end{cases}$$
这样矩阵每一行乘以R,就得到了新的PR值,比如第二行(图1的节点B),
$$\begin{align}
M_{2j} &=\ell(p_2,p_1)⋅PR(p_2)+\ell(p_2,p_2)⋅PR(p_2)+⋯+\ell(p_2,p_N)⋅PR(p_2)\
&=0 (‘A’)+0 (‘B’)+1 (‘C’)+12 (‘D’)+13 (‘E’)+12 (‘F’) +12 (‘G’)+12 (`H’)+12 (‘I’)+0 (‘J’)+0 (‘K’)
\end{align}$$
以节点G为例,G给B和E投票,所以B得到1/2。
矩阵M每一列加起来都是1(值得注意的是,对于没有出链的节点,列加起来等于0,比如图1的节点A),即
$$\sum_{i=1}^{N}\ell(p_i,p_j)=1$$。事实上,M是一个转移矩阵transition matrix(也叫概率矩阵probability matrix,马尔可夫矩阵Markov matrix)。因此,PageRank是eigenvector centrality的一个变体。
矩阵M
事实上,M可以被看成normalized的图邻接矩阵,即:
$$M=(K^{−1}A)^T$$
其中,A为图的邻接矩阵,以图1为例,1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# Get adjacency matrix
nodelist = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'] # sorted(G.nodes())
A = nx.to_numpy_matrix(G, nodelist)
'A' 'B' 'C' 'D' 'E' 'F' 'G' 'H' 'I' 'J' 'K'
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 1. 0. 1. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]]
A是对角矩阵,对角线上的元素是对应节点的出度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15nodelist = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'] # sorted(G.nodes())
list_outdegree = map(operator.itemgetter(1), sorted(G.out_degree().items()))
K = np.diag(list_outdegree)
[[0 0 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0 0 0 0]
[0 0 0 2 0 0 0 0 0 0 0]
[0 0 0 0 3 0 0 0 0 0 0]
[0 0 0 0 0 2 0 0 0 0 0]
[0 0 0 0 0 0 2 0 0 0 0]
[0 0 0 0 0 0 0 2 0 0 0]
[0 0 0 0 0 0 0 0 2 0 0]
[0 0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 0 1]]
K的逆矩阵$$K^{-1}$$为,1
2
3
4
5
6
7
8
9
10
11
12
13K_inv = np.linalg.pinv(K)
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0.5 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0.33 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0.5 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0.5 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0.5 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0.5 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. ]]
那么,根据公式$$M=(K^{−1}A)^T$$就可以求得M,如下,1
2
3
4
5
6
7
8
9
10
11
12
13M = (K_inv * A).transpose()
[[ 0. 0. 0. 0.5 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 1. 0.5 0.33 0.5 0.5 0.5 0.5 0. 0. ]
[ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0.33 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0.5 0.5 0.5 0.5 1. 1. ]
[ 0. 0. 0. 0. 0.33 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]
求解
R是2.1等式的特征向量(eigenvector),求解等式得:
$$\mathbf{R} = (\mathbf{I}-d \mathcal{M})^{-1} \frac{1-d}{N} \mathbf{1},$$
其中$$\mathbf{I}$$是单位矩阵。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15d = 0.85
I = np.identity(N)
R = np.linalg.pinv(I - d*M) * (1-d)/N * column_vector
[[ 0.028]
[ 0.324]
[ 0.289]
[ 0.033]
[ 0.068]
[ 0.033]
[ 0.014]
[ 0.014]
[ 0.014]
[ 0.014]
[ 0.014]]
咦,结果怎么跟图1不一样。得到R需要normalized,如此,所有节点的PR加起来才能等于1。1
2
3
4
5
6
7
8
9
10
11
12
13R = R/sum(R) # normalized R, so that page ranks sum to 1.
[[ 0.033]
[ 0.384]
[ 0.343]
[ 0.039]
[ 0.081]
[ 0.039]
[ 0.016]
[ 0.016]
[ 0.016]
[ 0.016]
[ 0.016]]
用NetworkX作出来的图,是这样的:
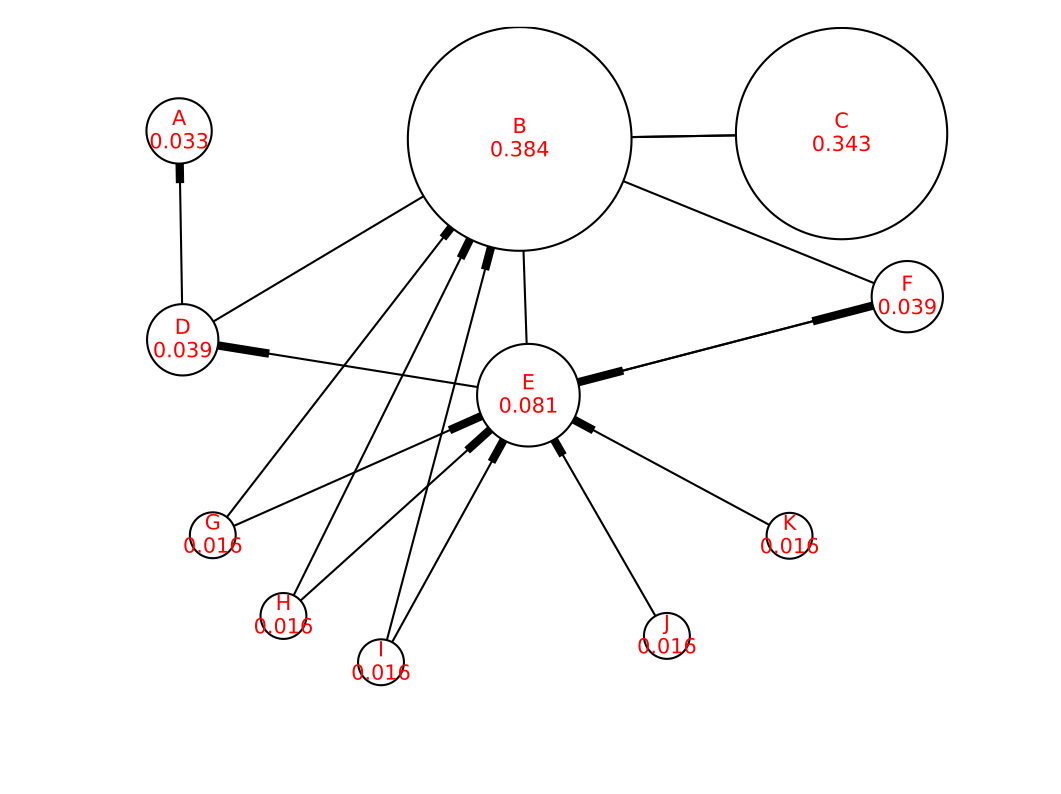
Fig. 3: PageRanks for a simple network
Python源代码
NetworkX实现了PageRank的代数计算方法nx.pagerank_numpy,源代码在这里。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def pagerank_numpy(G, alpha=0.85, personalization=None, weight='weight', dangling=None):
"""Return the PageRank of the nodes in the graph.
"""
if len(G) == 0:
return {}
M = google_matrix(G, alpha, personalization=personalization,
weight=weight, dangling=dangling)
# use numpy LAPACK solver
eigenvalues, eigenvectors = np.linalg.eig(M.T)
ind = eigenvalues.argsort()
# eigenvector of largest eigenvalue at ind[-1], normalized
largest = np.array(eigenvectors[:, ind[-1]]).flatten().real
norm = float(largest.sum())
return dict(zip(G, map(float, largest / norm)))
References: