迪菲-赫尔曼密钥交换
迪菲-赫尔曼密钥交换(英语:Diffie–Hellman key exchange,缩写为D-H)
最简单,最早提出的这个协议使用一个质数$p$的整数模$n$乘法群以及其原根$g$。
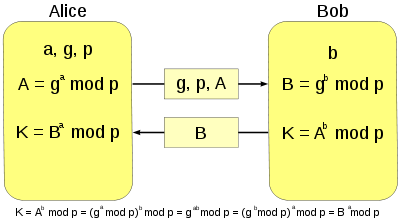
迪菲-赫尔曼密钥交换
算法如下(绿色表示非秘密信息, 红色粗体表示秘密信息):
- 爱丽丝与鲍伯协定使用 $$p=23$$以及base $$g=5$$.
- 爱丽丝选择一个秘密整数$$a=6$$, 计算$$A = g^a mod p$$并发送给鲍伯。
$$A = 56 mod 23 = 8$$.
- 鲍伯选择一个秘密整数$$b=15$$, 计算$$B = g^b mod p$$并发送给爱丽丝。
$$B = 515 mod 23 = 19$$.
- 爱丽丝计算$$s = B^a mod p$$
$$196 mod 23 = 2$$.
- 鲍伯计算$$s = A^b mod p$$
$$815 mod 23 = 2$$.
以下是一个更为一般的描述:
- 爱丽丝和鲍伯写上一个有限循环群 $$G$$ 和它的一个生成元 $$g$$。 (这通常在协议开始很久以前就已经规定好; $$g$$是公开的,并可以被所有的攻击者看到。)
- 爱丽丝选择一个随机自然数 $$a$$ 并且将$${\displaystyle g^{a}{\bmod {p}}} g^{a} \bmod{p}$$发送给鲍伯。
- 鲍伯选择一个随机自然数 $$b$$ 并且将$${\displaystyle g^{b}{\bmod {p}}} g^{b} \bmod{p}$$发送给爱丽丝。
- 爱丽丝 计算 $${\displaystyle \left(g^{b}\right)^{a}{\bmod {p}}} \left ( g^{b} \right )^{a} \bmod{p} $$。
- 鲍伯 计算 $${\displaystyle \left(g^{a}\right)^{b}{\bmod {p}}} \left ( g^{a} \right )^{b} \bmod{p} $$。
爱丽丝和鲍伯就同时协商出群元素$$ {\displaystyle g^{ab}} g^{ab} $$,它可以被用作共享秘密。
$${\displaystyle \left(g^{b}\right)^{a}} \left ( g^{b} \right )^{a} = {\displaystyle \left(g^{a}\right)^{b}} \left ( g^{a} \right )^{b}$$因为群是乘法交换的。