RNN

0.总结

本文主要讲了N vs N，N vs 1、1 vs N、N vs M四种经典的RNN模型，以及如何使用Attention结构。

---

1.从单层网络谈起

在学习RNN之前，首先要了解一下最基本的单层网络，它的结构如图：

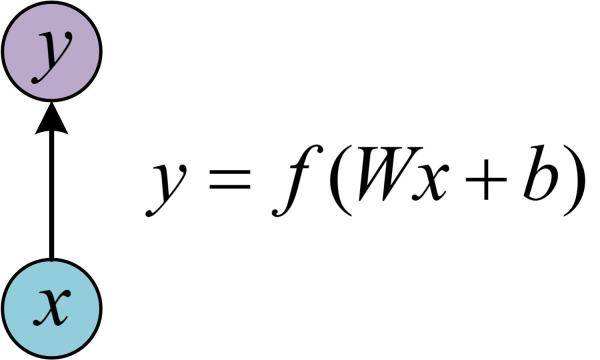
输入是x，经过变换Wx+b和激活函数f得到输出y

---

2.经典的RNN结构(N vs N)

在实际应用中，我们还会遇到很多序列形的数据：

如：

• 自然语言处理问题．x1可以看做是第一个单词，x2可以看做是第二个单词，依次类推。
• 语音处理．此时，x1、x2、x3……是每帧的声音信号。
• 时间序列问题．例如每天的股票价格等等

序列形的数据就不太好用原始的神经网络处理了。

为了建模序列问题，RNN引入了隐状态h（hidden state）的概念，h可以对序列形的数据提取特征，接着再转换为输出。

先从h1的计算开始看：

图示中记号的含义是：

• 圆圈或方块表示的是向量
• 一个箭头就表示对该向量做一次变换。如上图中h0和x1分别有一个箭头连接，就表示对h0和x1各做了一次变换。

在很多论文中也会出现类似的记号，初学的时候很容易搞乱，但只要把握住以上两点，就可以比较轻松地理解图示背后的含义。

h2的计算和h1类似。要注意的是，在计算时，每一步使用的参数U、W、b都是一样的，也就是说每个步骤的参数都是共享的，这是RNN的重要特点，一定要牢记。

依次计算剩下来的（使用相同的参数U、W、b）：

我们这里为了方便起见，只画出序列长度为4的情况，实际上，这个计算过程可以无限地持续下去。

我们目前的RNN还没有输出，得到输出值的方法就是直接通过h进行计算：

正如之前所说，一个箭头就表示对对应的向量做一次类似于f(Wx+b)的变换，这里的这个箭头就表示对h1进行一次变换，得到输出y1。

剩下的输出类似进行（使用和y1同样的参数V和c）：

OK！大功告成！这就是最经典的RNN结构，我们像搭积木一样把它搭好了。它的输入是x1, x2, …..xn，输出为y1, y2, …yn，也就是说，输入和输出序列必须要是等长的。

由于这个限制的存在，经典RNN的适用范围比较小，但也有一些问题适合用经典的RNN结构建模，如：

• 计算视频中每一帧的分类标签:因为要对每一帧进行计算，因此输入和输出序列等长。
• 输入为字符，输出为下一个字符的概率。
• 这就是著名的Char RNN（详细介绍请参考：The Unreasonable Effectiveness of Recurrent Neural Networks，Char RNN可以用来生成文章，诗歌，甚至是代码，非常有意思）。

---

3.N vs 1

有的时候，我们要处理的问题输入是一个序列，输出是一个单独的值而不是序列，应该怎样建模呢？

实际上，我们只在最后一个h上进行输出变换就可以了：

这种结构通常用来处理序列分类问题。

• 输入一段文字判别它所属的类别
• 输入一个句子判断其情感倾向
• 输入一段视频并判断它的类别等等。

---

4.1 VS N

输入不是序列而输出为序列的情况怎么处理？我们可以只在序列开始进行输入计算：

还有一种结构是把输入信息X作为每个阶段的输入：

下图省略了一些X的圆圈，是一个等价表示：

这种1 VS N的结构可以处理的问题有：

• 从图像生成文字（image caption），此时输入的X就是图像的特征，而输出的y序列就是一段句子
• 从类别生成语音或音乐等

---

5.N VS M

下面我们来介绍RNN最重要的一个变种：N vs M。

这种结构又叫Encoder-Decoder模型，也可以称之为Seq2Seq模型。

原始的N vs N RNN要求序列等长，然而我们遇到的大部分问题序列都是不等长的，如机器翻译中，源语言和目标语言的句子往往并没有相同的长度。

为此，Encoder-Decoder结构先将输入数据编码成一个上下文向量c：

得到c有多种方式，最简单的方法就是把Encoder的最后一个隐状态赋值给c，还可以对最后的隐状态做一个变换得到c，也可以对所有的隐状态做变换。

拿到c之后，就用另一个RNN网络对其进行解码，这部分RNN网络被称为Decoder。具体做法就是将c当做之前的初始状态h0输入到Decoder中：

还有一种做法是将c当做每一步的输入：

由于这种Encoder-Decoder结构不限制输入和输出的序列长度，因此应用的范围非常广泛，比如：

• 机器翻译:Encoder-Decoder的最经典应用，事实上这一结构就是在机器翻译领域最先提出的
• 文本摘要:输入是一段文本序列，输出是这段文本序列的摘要序列。
• 阅读理解:将输入的文章和问题分别编码，再对其进行解码得到问题的答案。
• 语音识别:输入是语音信号序列，输出是文字序列。
• …………

---

6.Attention机制

在Encoder-Decoder结构中，Encoder把所有的输入序列都编码成一个统一的语义特征c再解码。

因此， c中必须包含原始序列中的所有信息，它的长度就成了限制模型性能的瓶颈。

如机器翻译问题，当要翻译的句子较长时，一个c可能存不下那么多信息，就会造成翻译精度的下降。

Attention机制通过在每个时间输入不同的c来解决这个问题，下图是带有Attention机制的Decoder：

每一个c会自动去选取与当前所要输出的y最合适的上下文信息。

具体来说，我们用$$a_{ij}$$衡量Encoder中第j阶段的hj和解码时第i阶段的相关性，最终Decoder中第i阶段的输入的上下文信息$$ci$$就来自于所有$$a{ij}$$对的加权和。

以机器翻译为例（将中文翻译成英文）：

输入的序列是“我爱中国”，因此，Encoder中的h1、h2、h3、h4就可以分别看做是 “我” 、 “爱” 、 “中” 、 “国” 所代表的信息。

在翻译成英语时，第一个上下文c1应该和“我”这个字最相关，因此对应的就$$a{11}$$比较大，而相应的$$ a{12},a{13},a{14} $$就比较小。

c2应该和“爱”最相关，因此对应的$$ a{22} $$就比较大。最后的c3和h3、h4最相关，因此 $$ a{33},a_{34} $$的值就比较大。

至此，关于Attention模型，我们就只剩最后一个问题了，那就是：

这些权重$$ a_{ij} $$是怎么来的？

事实上，$$ a_{ij} $$同样是从模型中学出的，它实际和Decoder的第i-1阶段的隐状态、Encoder第j个阶段的隐状态有关。

同样还是拿上面的机器翻译举例，$$ a_{1j} $$的计算（此时箭头就表示对h’和$$ h_j $$同时做变换）：

$$ a_{2j} $$的计算:

$$ a_{3j} $$的计算:

Prev: jupyter-notebook-sen-usage

Next: Ubuntu的grub修复